Number Systems

Table of contents

  1. Decimal, Binary, and Hexadecimal
  2. Conversions Between Number Systems
    1. Decimal to Binary
    2. Decimal to Hexadecimal
    3. Decimal to Octal
  3. Binary, Octal, and Hexadecimal Shortcuts
    1. Binary to Octal:
    2. Octal to Binary:
    3. Binary to Hexadecimal:
    4. Hexadecimal to Binary:
  4. Fun With Number systems
    1. Using Python for Conversions
    2. Practice With Games!
  5. Why Learn About Number Systems?
    1. Decimal is Good for Humans
    2. Binary is Good for Computers
    3. Hexadecimal is Good for Programmers

Decimal, Binary, and Hexadecimal

We can represent numbers in different ways. Here examples:

  • Unary (Base 1): This number system uses a single digit (1) to represent any number. This is equivalent to counting using tally marks. For example, the number 5 in unary is represented as 11111. While this system is simple, it is not efficient for representing large numbers.

  • Decimal (Base 10): We can represent numbers using ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. This is the most common number system used in everyday life. Each digit’s position represents a power of 10. For example, \(123\) is calculated as: \((1\times10^2) + (2\times10^1) + (3\times10^0) = 100 + 20 + 3 = 123\), whereas \(231\) is calculated as: \((2\times10^2) + (3\times10^1) + (1\times10^0) = 200 + 30 + 1 = 231\).

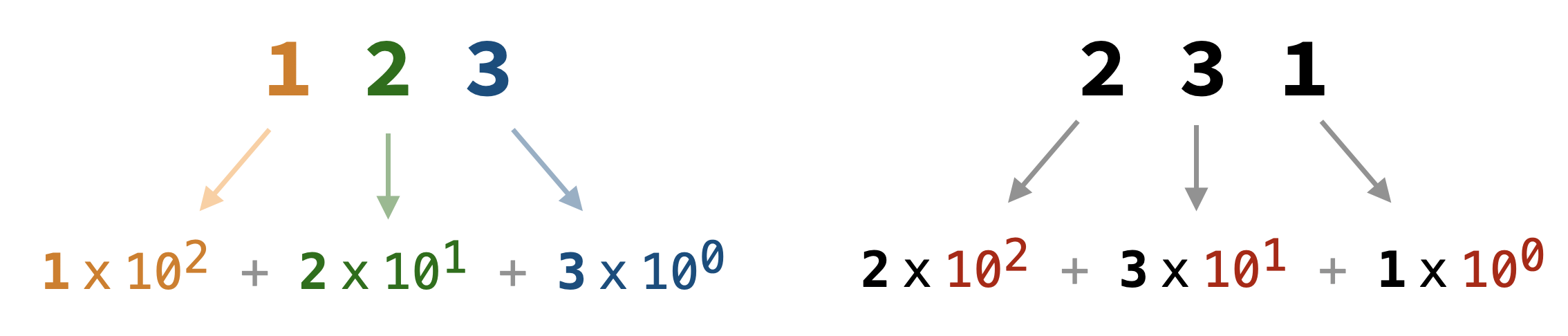
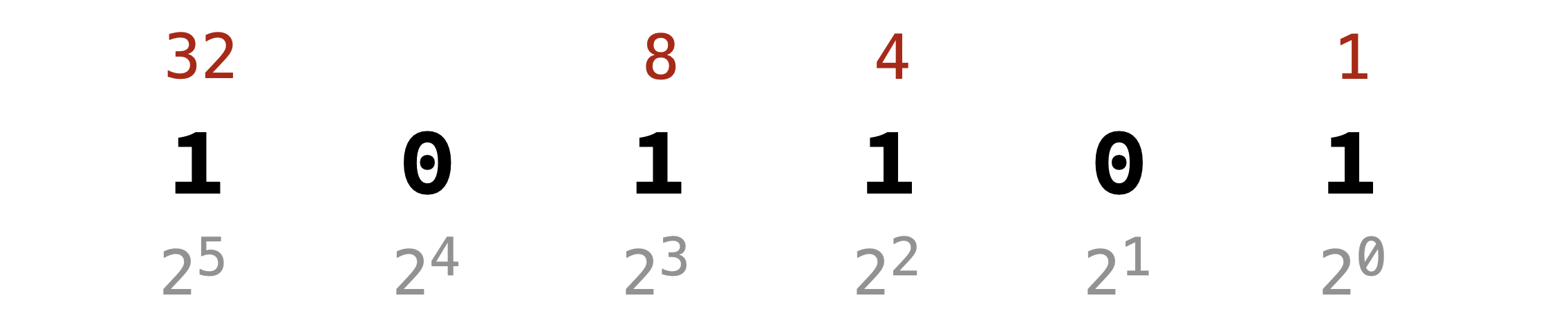
  • Binary (Base 2): This number system uses only two digits: 0 and 1. Each digit’s position represents a power of 2. For example, The number 101101 in binary represents:

\[(1\times2^5) + (0\times2^4) + (1\times2^3) + (1\times2^2) + (0\times2^1) + (1\times2^0) = 32 + 0 + 8 + 4 + 0 + 1 = 45\]
  • Hexadecimal (Base 16): This number system uses sixteen digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, where A to F represent the decimal values 10 to 15. Each digit’s position represents a power of 16. For example, The number 2E3F in hexadecimal represents:

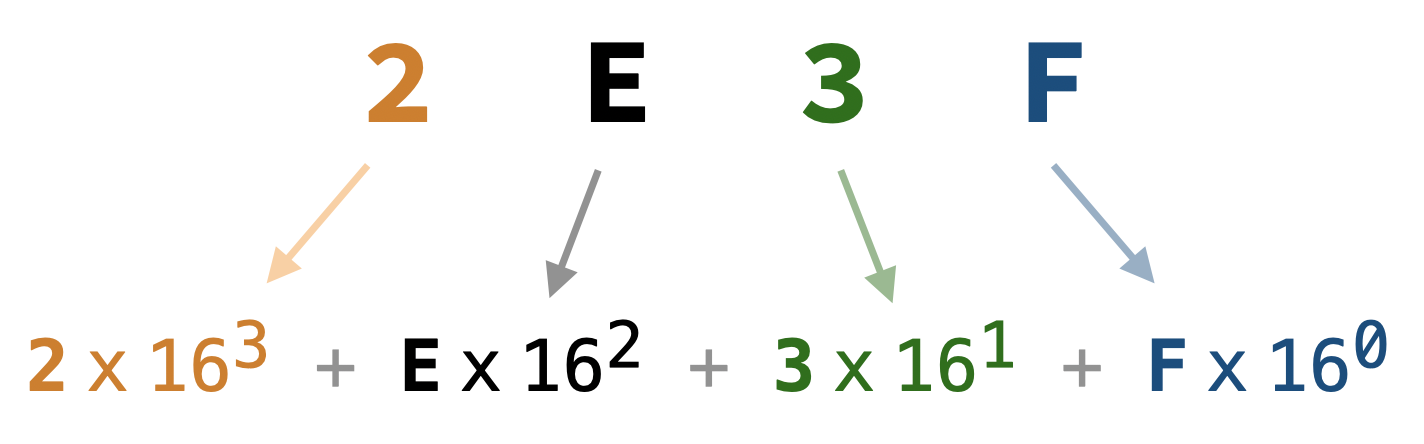
\[(2\times16^3) + (14\times16^2) + (3\times16^1) + (15\times16^0) = 8192 + 3584 + 48 + 15 = 11839\]
  • Octal (Base 8): This number system uses eight digits: 0, 1, 2, 3, 4, 5, 6, 7. Each digit’s position represents a power of 8. For example, The number 345 in octal represents:
\[(3\times8^2) + (4\times8^1) + (5\times8^0) = 192 + 32 + 5 = 229\]

Conversions Between Number Systems

The examples above show how to convert from other number systems to decimal. Below are methods to convert from decimal to other number systems.

Decimal to Binary

Intutively, we need to find which powers of 2 add up to the given decimal number. Watch the following two videos for detailed explanations:

A more systematic way to convert decimal to binary is by repeatedly dividing the number by 2 and keeping track of the remainders.

Example 1: Convert 13 to binary.

1.   13 / 2 = 6    remainder 1
2.    6 / 2 = 3    remainder 0
3.    3 / 2 = 1    remainder 1
4.    1 / 2 = 0    remainder 1

Reading the remainders in reverse order gives us 1101. Therefore, 13 in decimal is 1101 in binary.

Example 2: Convert 45 to binary.

1.   45 / 2 = 22    remainder 1
2.   22 / 2 = 11    remainder 0
3.   11 / 2 = 5     remainder 1
4.    5 / 2 = 2     remainder 1
5.    2 / 2 = 1     remainder 0
6.    1 / 2 = 0     remainder 1

Reading the remainders in reverse order gives us 101101. Therefore, 45 in decimal is 101101 in binary.

Decimal to Hexadecimal

Just like binary, we can convert decimal to hexadecimal by repeatedly dividing the number by 16 and keeping track of the remainders.

Example 1: Convert 755 to hexadecimal.

1.   755 / 16 = 47   remainder 3
2.    47 / 16 = 2    remainder 15 (`F` in hexadecimal)
3.     2 / 16 = 0    remainder 2

Reading the remainders in reverse order gives us 2F3. Therefore, 755 in decimal is 2F3 in hexadecimal.

Example 2: Convert 11839 to hexadecimal.

1.  11839 / 16  = 739    remainder 15 (`F` in hexadecimal)
2.    739 / 16  = 46     remainder 3
3.     46 / 16  = 2      remainder 14 (`E` in hexadecimal)
4.      2 / 16  = 0      remainder 2

Reading the remainders in reverse order gives us 2E3F. Therefore, 11839 in decimal is 2E3F in hexadecimal.

Decimal to Octal

Now, you should be able to convert decimal to octal using the same method of repeated division, but this time dividing by 8.

Example 1: Convert 229 to octal.

1.  229 / 8 = 28    remainder 5
2.   28 / 8 = 3     remainder 4
3.    3 / 8 = 0     remainder 3

Reading the remainders in reverse order gives us 345. Therefore, 229 in decimal is 345 in octal.

Binary, Octal, and Hexadecimal Shortcuts

Since 2, 8, and 16 are all powers of 2, we can convert between binary and octal/hexadecimal more easily.

Binary to Octal:

Group the binary digits into sets of three (starting from the right) and convert each group to its octal equivalent.

Example: Convert 10111011 to octal.

  1. Group into sets of three: 010 111 011. Note that we added a leading zero to make a complete group of three.
  2. Convert each group:
    • 010 (binary) = 2 (octal)
    • 111 (binary) = 7 (octal)
    • 011 (binary) = 3 (octal)
     Octal:    2     7     3
    Binary:   010   111   011

Reading the octal digits gives us 273. Therefore, 10111011 in binary is 273 in octal.

Octal to Binary:

Convert each octal digit to its three-digit binary equivalent.

Example: Convert 427 to binary.

  • 4 (octal) = 100 (binary)
  • 2 (octal) = 010 (binary)
  • 7 (octal) = 111 (binary)
Octal:        4     2     7
    Binary:   100   010   111

Reading the binary digits gives us 100 010 111. Therefore, 427 in octal is 100010111 in binary.

Binary to Hexadecimal:

Group the binary digits into sets of four (starting from the right) and convert each group to its hexadecimal equivalent.

Example: Convert 11010111001010 to hexadecimal.

  1. Group into sets of four: 0011 0101 1100 1010. Note that we added leading zeros to make a complete group of four.
  2. Convert each group:
    • 0011 (binary) = 3 (hexadecimal)
    • 0101 (binary) = 5 (hexadecimal)
    • 1100 (binary) = C (hexadecimal)
    • 1010 (binary) = A (hexadecimal)
Hexadecimal:    3     5     C     A
    Binary:     11  0101  1100  1010

Reading the hexadecimal digits gives us 35CA. Therefore, 11010111001010 in binary is 35CA in hexadecimal.

Hexadecimal to Binary:

Convert each hexadecimal digit to its four-digit binary equivalent.

Example: Convert 3AF to binary.

  • 3 (hexadecimal) = 0011 (binary)
  • A (hexadecimal) = 1010 (binary)
  • F (hexadecimal) = 1111 (binary)
Hexadecimal:      3     A     F
    Binary:     0011  1010  1111

Reading the binary digits gives us 0011 1010 1111. Therefore, 3AF in hexadecimal is 001110101111 in binary.

Here is a video summary of the conversions between binary and hexadecimal:

Having the following table ready might help with conversions:

Fun With Number systems

Using Python for Conversions

Open a Python interactive shell (REPL) and type the following statmeents:

bin(45)                # '0b101101'
bin(45)[2:]            # '101101' (removes the '0b' prefix)

hex(11839)             # '0x2e3f'
hex(11839)[2:]         # '2e3f' (removes the '0x' prefix)
hex(755)[2:].upper()   # '2F3'

oct(229)               # '0o345'
oct(229)[2:]           # '345' (removes the '0o' prefix)

int('101101', 2)       # 45
int('2E3F', 16)        # 11839
int('345', 8)          # 229

When using the int() function to convert from other number systems to decimal, you need to specify the base as the second argument.

Practice With Games!

Here are two fun games to practice converting between number systems:

Why Learn About Number Systems?

Decimal is Good for Humans

As you might have noticed, the higher the base of the number system, the fewer digits are needed to represent large numbers. Therefore, we can be very efficient in representing numbers if we use a higher base number system (e.g., base 100). However, higher base number systems are harder to work with.

We humans, use the decimal (base 10), which provides a good balance between efficiency and ease of use. It is much more efficient than unary and binary, yet it is much easier to work with than hexadecimal or octal, probably because we have ten fingers.

Binary is Good for Computers

Using decimal numbers on computers is possible, but requires complex hardware and software to represent 10 different states (0-9) reliably. Instead, computers use binary (base 2), which only requires two states (0 and 1). This makes it much easier to design reliable hardware, where one state can be modeled as OFF (no power) and the other as ON (power).

Hence, understanding binary and how to convert between number systems is essential for working with computers and programming. You will see next, how all types of data (numbers, text, images, videos, etc.) are represented using binary in computers.

Hexadecimal is Good for Programmers

While we need to work with binary in computers, binary numbers can get very long and hard to read. Also, converting between binary and decimal can be tedious. Therefore, programmers often use hexadecimal (base 16) as a middle ground. Hexadecimal is more compact than binary, making it easier to read and write, while still being relatively easy to convert to and from binary as we saw earlier.

© Ibrahim Albluwi. · Last updated: